Колмогоровские Летние Школы

Школа-интернат №18 при МГУ им. М.В. Ломоносова была открыта 2 декабря 1963 года. Однако подготовка к ее открытию началась весной 1963 года, когда победителей третьей Всероссийской олимпиады школьников пригласили в подмосковное Красновидово в летнюю школу. Всего в эту летнюю школу приехало 46 учащихся, 19 из которых и составили первый набор учеников интерната - самый первый класс школы, а затем и первый выпуск школы. Мы очень гордимся этим выпуском, многие из этих первых выпускников стали выдающимися учеными и с большинством из них школа поддерживает контакты до настоящего времени.

По предложению Андрея Николаевича Колмогорова (одного из основных инициаторов создания школ при университетах страны), именно так, много лет и осуществлялся набор учащихся в школу при МГУ: основная масса кандидатов на зачисление в школу (по итогам вступительных экзаменов) приглашалась на обучение в трехнедельную летнюю физико-математическую школу (ЛФМШ), проводимую механико-математическим и физическим факультетами университета и школой-интернатом; при этом вся организация работы летней школы и другие многочисленные хлопоты целиком лежали на спецшколе. По итогам работы в летней школе и происходило окончательное зачисление учеников. Те участники летних школ, которые по тем или иным причинам не поступили в школу-интернат не теряли время зря, а получали неизгладимое впечатление от той атмосферы увлеченности делом, которая всегда присуща таким школам, получили добротные знания, имели возможность постоянных контактов как с маститыми учеными, так и с молодыми способными аспирантами и студентами. Справедливости ради нужно отметить, что в «Положении о специализированной школе-интернате при государственном университете», на основании которого школа жила вплоть до 1988 года, ничего не было сказано о летних школах; дословно было предписано так: «Отбор кандидатов на зачисление в специализированную школу-интернат производится университетом совместно с органами народного образования на основе конкурсных экзаменов по профилирующим дисциплинам и собеседования ученых с поступающими, с учетом рекомендации педагогического совета школы». Поэтому проведение летних школ накладывало на Университет ежегодное дополнительное финансовое бремя, так как в бюджет школы такой фрагмент ее деятельности заложен не был, а деньги для этого требуется большие. В 1988 году школа-интернат изменила свой статус - на ее основе был создан Специализированный учебно-научный центр МГУ как самостоятельное подразделение университета, а школа-интернат в этот центр вошла как школа им. академика А.Н. Колмогорова.

В летних физико-математических школах пяти(шести)дневная рабочая неделя и система занятий, как правило, лекционно-семинарская. Лекций немного: 1-2 часа по каждому предмету в неделю. Учащиеся занимаются 6 часов: четыре часа до обеда и два часа после обеда. Традиционно проводятся различные олимпиады и тестирования. Дополнительно к обязательным занятиям для особо интересующихся школьников работает несколько кружков. В каждой группе работают два - три преподавателя математики, которые одновременно присутствуют на занятиях, так что во время работы на уроке преподаватель беседует с каждым школьником несколько раз. Тесное общение между преподавателями и школьниками, конечно, не ограничивается только уроками, школьники в любое время могут получить нужную консультацию. Благодаря такой организации, занятия в ЛФМШ проходят в атмосфере дружбы, взаимопонимания и увлеченности. Отметим, что летние математические школы в один из каникулярных месяцев – это не только время для занятия математикой и в них никогда не забывают о спорте и туризме, об отдыхе, об экскурсиях и беседах на музыкальные, литературные (другие, самые разнообразные) темы. Поэтому очень важен состав преподавателей, воспитателей и других «взрослых», которые проводят занятия и организуют всю жизнь летней школы. Основными преподавателями (лекторами) летних школ являются профессора и доценты университета, а молодые преподаватели подбираются из числа способных студентов и аспирантов, бывших участников олимпиад, обладающих своими ярко выраженными интересами, любящих спорт и работу с талантливыми школьниками.

А.Н. Колмогоров работал в Красновидовских летних школах в 1963, 1964, 1965, 1968 и 1970 годах, в г. Пущино на Оке – в 1971, 1972, 1975 и 1977 годах.

О первой летней школе в Красновидово в 1962 году, которая прошла на базе отдыха МГУ, хорошо рассказал ее участник Александр Абрамов, ставший потом, учащимся первого набора школы-интерната, выпускником механико-математического факультета МГУ и его аспирантуры, защитившим кандидатскую диссертацию под руководством А.Н. Колмогорова, членом-корреспондентом Российской Академии Образования. Мы приведем здесь полностью выдержку из его воспоминаний (см.[6]) об этой летней школе: «…Одновременно велось несколько основных курсов, из которых нужно было выбрать два обязательных – по ним предстояло сдать зачет… А.Н. Колмогоров читал курс (примерно 10 уроков) «Конечные поля и булевы алгебры», завершившийся примерами применения булевой логики к задачам построениях контактных схем. П.С. Александров прочел курс по теории множеств. В.И. Арнольд вел продвинутую группу, в которую вошли ребята, уже знакомые с понятиями анализа; А.Г. Кушниренко и А.М. Леонтович (тогда студенты) вели занятия с группой начинающих. Н.Х. Розов и О.Н. Найда занимались механикой, а А,А. Карацуба – теорией чисел. Особенностью семинарских занятий было одновременное участие двух или даже трех молодых преподавателей (среди них А.С. Мищенко, М.Л. Гервер, А.Л. Тоом), занимавшихся с учащимися индивидуально. Кроме того, велись кружки, читались отдельные лекции.

Занятия, естественно, сопровождались упражнениями. Постоянно вывешивались списки задач, учитывающие все вкусы. В любое время можно был, встретив преподавателя (и Андрея Николаевича в том числе), задать вопрос, получить консультацию. Ученикам и преподавателям выдавались краткие конспекты лекций…

По вечерам регулярно устраивались музыкальные или литературные вечера, велись беседы учеников с молодыми преподавателями на самые волнующие школьников темы, собственно математические или же связанные с поступлением в университет. Популярностью пользовались «английские шарады», логические игры. Обязательные утренние зарядки и ежедневные купания три раза в день при любой погоде, погоды в лес, заплыв через Московское море, «флагманами» которого были П.С. Александров и А.Н. Колмогоров, экскурсия на Бородинское поле – вот штрихи красновидовского лета…».

Содержание курсов в летней школе всегда отбирается так, чтобы разница в уровне подготовки учащихся как можно меньше сказывалась на результатах их работы в ЛФМШ. Отбор учебных материалов происходит таким образом, чтобы обучение было интересным и доступным для всех, а его изучение создавало атмосферу поиска, увлеченности и развития интереса к проведению, пусть небольших, работ исследовательского характера. По каждому предмету проводятся контрольные работы, а в конце – зачеты. ЛФМШ является удобной базой для экспериментирования с содержанием и методикой обучения школьников, интересующихся математикой и физикой и поэтому в летней школе нет раз и навсегда заданных программ. При этом, организаторы таких школ, конечно, учитывают имеющиеся у школьников знания, но стремятся не затрагивать те разделы школьной программы, которые учащимся в дальнейшем еще предстоит изучить, а если уж такие темы и включаются, то они рассматриваются с других позиций.

В 50 километрах от Иванова находится Рубское озеро, на берегах которого Ивановский пединститут имеет сою спортивно-оздоровительную базу. Здесь и была организована в июле 1968 года работа летней физико-математической школы, в которую были приглашены 60 школьников из Ивановской и Ярославской областей и 20 человек были направлены приемной комиссией школы-интерната при МГУ из числа окончивших восьмые классы в сельских школах в других областях и поступающих на учебу в интернат. Здесь были, в основном, учащиеся окончившие восьмой (ныне девятый) класс и с самого начала было решено, что около 30 участников летней школы получат направление на продолжение обучения в школе при МГУ. Отметим, что прием в эту школу детей из Ивановской и Ярославской областей в этом году проходил только через летнюю школу на Рубском озере. Организационно все происходило как и в других летних школах, но, конечно, со своей спецификой. Утро каждого дня начиналось с короткой линейки и зарядки, а потом - купание по желанию. Многие из участников школы увлеклись этими купаниями и были внесены даже некоторые запреты на их продолжительность и дальность заплывов. С 9 до 12 часов – лекция и два часа практических занятий. Затем спортивные игры, обед, прогулки в лес, а с 16 часов проводилось еще 2-3 часа учебных занятий. В послеобеденные часы проводились семинарские занятия, работали кружки, проходили консультации, олимпиады. Вечер – для самостоятельных занятий, катания на лодках, отдыха и пр. Запомнилась поездка в Суздаль и большинство из школьников были здесь впервые. А.Н. Колмогоров изумлял всех своими познаниями в архитектуре и рассказами о великих зодчих. В школе были три дисциплины, которые назывались «Алгебра», «Геометрия» и «Физика».

Курсом алгебры руководил А.Н. Колмогоров. В программе этого курса было несколько разделов. Первый из них назывался «Функция и ее график», в котором вводилось общее понятия функции как отображения, понятие обратной функции, рассматривались геометрические преобразования с функциональной точки зрения. Вторая глава этого раздела была посвящена функциям двух и многих переменных, другим зависимостям между переменными и их графикам, системам уравнений и неравенств.. Заключительная часть была посвящена методам решения алгебраических уравнений при помощи номограмм. Здесь проводились групповые занятия (математические практикумы) и многие учащиеся выполняли довольно значительный объем графической и чертежной работы и давали к полученным «картинкам» интересные и довольно глубокие пояснения теоретического характера. Курс «Геометрии» состоял из четырех лекций, посвященных построению геометрии из аксиоматики Г. Вейля и трех лекций по линейному программированию. Лекции читали профессор Ивановского педагогического института С.В. Смирнов и старший преподаватель этого же института Г. В. Пухова. Учащиеся впервые здесь увидели, как можно получить известные им уже геометрические факты при помощи формальных средств из немногих аксиом. На примере простейших задач линейного программирования было показано, как математика применяется в задачах реального прикладного содержания. Все учащиеся участвовали в проведении измерительных работ на местности, занимаясь съемкой плана берегов озера, которыми руководил И.Г. Журбенко. Это пришло из интернатских московских стен, в которых эти работы уже проводились (например, измеряли расстояние от школы до МГУ). Одна группа школьников наносили на план некоторые основные точки на его берегах, другая группа объезжая озеро, уточняли этот план. Это было довольно увлекательно, так как было сопряжено с поездками на лодках и с самостоятельным изготовлением измерительных приборов. Каждую субботу проводилась олимпиада. Она не была обязательной, но в них с большим удовольствием участвовали все школьники.

Расскажу также о летней школе 1977 года, которая проходила в г. Пущино-на-Оке на базе филиала МГУ и на организацию работы этой самой многочисленной ЛШ было потрачено много сил - на нее было приглашено около 250 школьников из многих регионов страны (см. [1],[3],[5]. Из числа преподавателей математики в ней работали: А.Н. Колмогоров, Ю.П. Соловьев, В.Н. Чубариков, В.В. Никулин, А.А. Егоров, В.В. Вавилов, А.Н. Земляков, В.В. Рождественский, С.А. Богатый, В.В. Годованчук, Л.В. Богачев, О.В. Селезнев, В.А. Чулаевский, В.К. Семина, В.В. Плескунин, С.Н. Артемов, О.Р. Мусин, В.Г. Никитенко, Л.Г. Ветров, Л.Н. Фахретдинова, Н.В. Теплова, Р.М. Давлетов, Т.Н. Трушанина, Н.М. Бовт, Б.М. Ивлев, В.Ф. Пахомов, О.В. Ляшко, Д.И. Гордеев, И.К. Светличнова, Т.П. Старкина (некоторые из них были с семьями, другие - не полный срок). Андрей Николаевич был со своей женой Анной Дмитриевной, Д.И. Гордеев с сыном Денисом, В.В. Рождественский был с женой, были также другие дети и родственники. Анна Дмитриевна попросила мою жену помочь ей по хозяйству, но когда узнала, что она беременна, то свою просьбу отменила.

В этой школе было два учебных математических курса: Алгебра и начала анализа (лекторы: А.Н. Колмогоров, В. В. Вавилов и В.В.Рождественский) и геометрия (лекторы: А.Н. Земляков и Ю.П.Соловьев), руководили разнообразными кружками и проводили математические практикумы. Преподаватели «оккупировали» обе гостиницы в Пущино, школьники – филиал общежития МГУ. Возле гостиниц находятся очень живописные крутой берег Оки, на другом берегу – известный Серпуховской заповедник. Кстати именно тогда там снимался один из эпизодов фильма «Несколько дней из жизни Обломова» и шумная съемочная группа Н. Михалкова жила в той же гостинице, которые постоянно извинялись перед А.Н. Колмогоровым. В одном из номеров жил довольно известный музыкант Д.В. Шебалин, которого А.Н. Колмогоров пригласил как-то на чай к себе в номер, где обсуждались не только музыкальные темы, но и проблемы школьного образования. Кафе «Нептун» на высоком берегу Оки постоянно было постоянно заполнено людьми, связанными с летней школой, и его посетители услышали тогда много «нетипичных застольных» разговоров о математике, физике, о трудностях преподавания и пр.

Курс А.Н. Колмогорова для 9-х классов (ныне десятых) «Дифференциальные уравнения» состоял из 5 лекций. Его содержание сводилось (материалы сохранились) к следующему: Задача о камне, брошенном вверх. Радиоактивный распад. Первообразная и интеграл. Формула Ньютона-Лейбница. Задача о прыгающем мячике. Гармонические колебания. Векторзначные функции и их производные. Циклоида. Теория часов (практикум). Начало этого курса полностью соответствовало материалу школьного учебника. Однако уже на первой лекции ставилась задача о расчете движения не вполне упругого мяча, отскакивающего от пола, которая приводит к обобщению понятия первообразной для функции с конечным числом разрывов. Отталкиваясь от дифференциального уравнения y’ =ky, был рассмотрен целый ряд задач, приводящих к этому уравнению: радиоактивный распад, ядерное деление, движение с трением и т.д. Возникающие в кинематике векторнозначные функции действительной переменной – третья тема курса. Годографы таких функций и годографы скорости и ускорения с были предметом специального чертежного практикума. При анализе дифференциального уравнения гармонических колебаний y’’=y вводилась так называемая фазовая плоскость, а само дифференциальное уравнение записывалось в векторном виде. Используя уже имеющиеся сведения о производных векторнозначных функций, отыскивались все решения исходного дифференциального уравнения, а затем и более общего вида. Все занятия сопровождались объемными графическими заданиями (практикумами).

Курс А.Н. Землякова «Комбинаторика и теория групп» был посвящен группам самосовмещений правильных многоугольников и многогранников. Его содержание было таково: 1) Отображения и подмножества конечных множеств. Сочетания, перестановки, размещения, разбиения; 2) Группы вращений плоских и пространственных фигур. Комбинаторика раскрасок; 3) Группы подстановок. Общее понятие группы и подгруппы. Представление об изоморфизме групп.

В начале этого курса изучались элементы комбинаторики, анализируя задачи о числе отображений конечных множеств, о числе подмножеств данного множества, об упорядоченных множествах, о разбиениях конечного множества на подмножества. Основная цель курса была – на доступном материале познакомить учащихся с одним из важнейших понятий современной алгебры – понятием группы. Тема начиналась с самых простых и наглядных примеров: групп самосовмещений (точнее, вращений) прямоугольника, куба, тетраэдра, правильных многоугольников. Интересными были задачи о числе геометрически различных раскрасок таких фигур. Интерпретируя вращения фигур с помощью перестановок вершин, отыскивались композиции поворотов, подводя учащихся ко второму основному примеру – группам подстановок. Группы подстановок изучались подробно: рассматривались разложения подстановок на циклы, отыскивались порядки подстановок, решались различные уравнения в группах подстановок в виде композиции транспозиций, приводящих к понятию образующих. Красивая иллюстрация этих понятий (образующих, четности подстановки) иллюстрировалась при построении математической теории игры «в пятнадцать». Среди привлекательных примеров приложений теории групп упомянем задачу о числе раскрасок вершин правильного р-угольника в n цветов, приводящую к малой теореме Ферма (при простом р число n^p – n делится на р); аналогично получается и теорема Вильсона (при простом р число (р-1)! + 1 делится на р. Математический практикум: орнаменты на плоскости.

В лекциях и на занятиях у Ю.П. Соловьева по теме «Геометрические преобразования», предназначенных восьмиклассникам (ныне девятиклассникам), в первой части подробно рассматривались перемещения плоскости – параллельные переносы, повороты, симметрии, скользящие симметрии. Исходя из группового свойства перемещений, детально изучались всевозможные композиции перемещений. Опорой здесь служило представление произвольного перемещения в в виде композиции не более трех осевых симметрий. Отсюда же с использованием аксиомы подвижности плоскости выводилась теорема Шаля о том, что любое перемещение плоскости является либо параллельным переносом, либо поворотом, либо осевой или скользящей симметрией. Задачи общего характера сочетались с разнообразными задачами на доказательство и построение, решение которых упрощается после применения свойств тех или иных перемещений. Основываясь на этом материале, далее рассматривались плоские орнаменты и группы их самосовмещений, так называемые плоские кристаллографические группы. Проводился практикум по вычерчиванию орнаментов и отысканию всех 17 плоских кристаллографических групп. При изучении свойств подобных фигур и преобразований подобия особое внимание уделялось приложению этих понятий к доказательству важных планиметрических теорем, в том числе теорем Чевы, Менелая, Птолемея и других. Этот курс вызвал самый живой интерес учащихся.Отметим, что как раз в это время готовилась к переизданию широко известная книга П.С. Александрова «Введение в теорию групп» и ее автор попросил Ю.П. Соловьева написать к ней специальное приложение. Отчасти и этим было вызвана та тщательность по проведению этого курса Ю.П. Соловьевым - вообще блестящим лектором, рассказчиком и популяризатором науки.

В.В. Вавилов и В.В. Рождественский (мы вели этот курс совместно), в основном, на своих лекциях занимались тематикой, связанной с функциями и методами построения их графиков. Его курс назывался «Функции и графики» и имел следующую программу: 1) Зависимости между двумя переменными и их графики. Системы уравнений и неравенств на плсокости. Линейное программирование; 2) Полярные координаты и графики. 3) Графическое исследование квадратичной функции. Линейные преобразования графиков. Дробно-линейные функции. Асимптоты. Графики квадратично-рациональных функций. Основной целью этого курса являлось изучение разнообразных типов функциональной зависимости на наглядно-графической основе. Помимо традиционных вопросов – методы построения графиков и их преобразования, графическое решение уравнений, неравенств и систем с одной и несколькими переменными и т.д., был подобран и нестандартный материал. Так, например, учащиеся с большим интересом вычерчивали кривые Уатта, «кривую дьявола» (х⁴ -96х² = у⁴ – 100у²), «розы и розетки», круговые циклоиды и их эволюты и т.п. При изучении квадратичной функции основное внимание уделялось отысканию на координатной плоскости множеств точек с координатами (p,q), которое соответствуют трехчленам x² + px + q с заданным свойствам корней. Композиции переносов и сжатий, позволяющие из графика функции y = f(x) получить график функции y = af(kx+l) + b, подробно рассматривались на примерах дробно-линейных и квадратично-рациональных функций. Итогом работы явилась полная классификация этих классов функций по типу их графиков, основанная на элементарных соображениях. Здесь было также несколько заданий практикума по вычерчиванию самого разного рода кривых.

О работе и содержании учебных курсов некоторых других ЛФМШ можно судить по воспоминаниям о летней школе в Красновидово [1, 6, 7 ], о летней школе на Рубском озере под г. Иваново 1970 года в [2], о летней школе, проводившейся на базе школы им. А.Н. Колмогорова в 1999 году в [8]; см. также [4], [5], [9].

Сейчас на базе школы им. А.Н. Колмогорова проводится Летняя олимпиадная школа и это становится уже традицией; это очень важное и полезное направление работы для школы им. А.Н. Колмогорова, продолжающее и развивающее идеи основоположника школы. В качестве одной из нереализованных задумок А.Н. Колмогорова отметим организацию летних (зимних) школ для учителей математики и руководителей школьных математических кружков. Эта идея, в таком рафинированном виде, пока не реализована нами широко. Отметим, что летних школ у нас в стране сейчас проводится большое количество и их формы проведения довольно разнообразны: как традиционные для школьников, так и специализированные летние семинары, тематические летние школы для студентов и аспирантов, летние школы по тем или иным областям современной математической науки и др. Такого рода деятельность школ, педагогических институтов и университетов страны заслуживает внимания и всяческих похвал.

Литература:

1. А.Н. Колмогоров, В.В. Вавилов, И.Т. Тропин, Физико-математическая школа при МГУ. – М.: Знание, 1981. (Новое в жизни, науке, технике. Сер. «Математика, кибернетика», №5).

2. А.Н. Колмогоров, И. Г. Журбенко, Г.В. Пухова, О.С. Смирнова, С.В. Смирнов, Летняя школа на Рубском озере. Из опыта работы летней физико-математической школы. –М.: Просвещение, 1971.

3. В.В. Вавилов, А.Н. Земляков, Из опыта работы летней физико-математической школы при МГУ. – Журнал «Математика в школе», 1978, №4.

4. В.В. Вавилов, Школа им. А.Н. Колмогорова Московского государственного университета им. М.В. Ломоносова. Сборник статей ко дню рождения А.Н. Колмогорова (Ред. коллегия: Часовских А.А., Вавилов В.В., Качалкин А.Н., Шивринская Е.В.). – М.: Научно-технический центр «Университетский», 2003.

5. В.В. Вавилов, Школа математического творчества. – М.: РОХОС, 2004.

6. А.М. Абрамов, О педагогическом наследии А.Н. Колмогорова. В книге: Явление чрезвычайное. Книга о Колмогорове. – М. ФАЗИС, МИРОС, 1999.

7. А.А. Егоров, А.Н. Колмогоров и колмогоровский интернат. В книге: Явление чрезвычайное. Книга о Колмогорове. – М. ФАЗИС, МИРОС, 1999.

8. В.Н. Дубровский, А.Б. Скопенков, А.В. Спивак, МАТЕМАТИКА, 10 класс. Материалы летней физико-математической школы. – М.: Школа им. А.Н. Колмогорова, 1999.

9. В.В. Вавилов, М. Е. Колоскова, Уроки в цветущем саду. – Учебно-методическая газета «Математика. 1сентября», 20(2006).

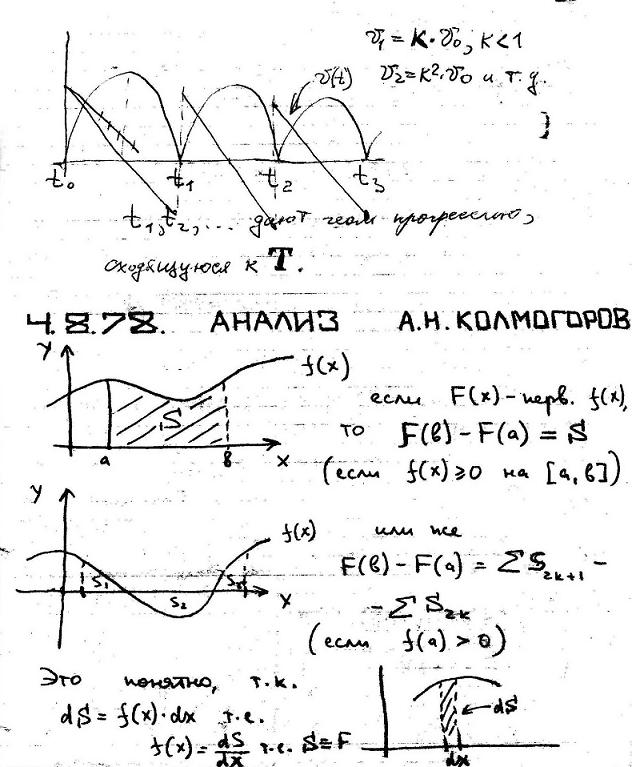
Из конспекта ученика летней школы в Пущино-на-Оке 1978 года

А.А. Егоров и В.В. Вавилов. ЛШ в Пущино на Оке, 1978