Поддержка и популяризация математического образования. Реализация проектов и программ обучения.

Исследовательские проекты для школьников

В этой рубрике мы публикуем те темы и циклы задач, которые могут стать предметом самостоятельного исследования школьников и послужить основой докладов на научных конференциях различных уровней. С успехом их можно также использовать при организации работы школьных кружков и олимпиад.

Лучшие работы учащихся будут опубликованы на сайте кафедры математики школы им. А.Н. Колмогорова и рекомендованы для публикации в различных научно-популярных и научных журналах.

Замечания по публикуемым материалам и новые предложения читателей будут встречены редакцией с большой благодарностью.

Дискретные гармонические функции

Научный руководитель:

к.ф.м.н., доцент Вавилов Валерий Васильевич (Школа им. А.Н. Колмогорова)

В каждый узел бесконечного листа клетчатой бумаги поместим действительное число так, чтобы любое число было бы равно среднему арифметическому чисел, стоящих в четырех соседних узлах бумаги. Другими словами, рассмотрим функцию двух переменных у = F(i,j), которая определена на всех целочисленных точках (i,j) и такую, что

F(i,j) = 1/4(F(i-1,j) + F(i+1,j) + F(i,j-1) + F(i,j+1))

для любых целых значений i и j. Такие функции у = F(i,j) называются дискретными гармоническими функциями.

На школьных олимпиадах, например, встречались такие две задачи:

А) (Москва). Доказать, что если дискретная гармоническая функция принимает только натуральные значения, то эта функция равна некоторой постоянной, т.е. все ее значения равны.

Б) (Ленинград). Доказать, что если рассмотреть любой прямоугольник с вершинами в узлах клетчатой бумаги и сторонами параллельными ее линиям, то наибольшее и наименьшее значение из числа тех, которые принимает дискретная гармоническая функция во внутренних и граничных узлах этого прямоугольника, находятся в граничных узлах.

Известна также следующая теорема Лиувилля, которую мы предлагаем в качестве задачи

С). Доказать, что если дискретная гармоническая функция ограничена, то она постоянна.

Одним из центральных является следующий вопрос: Верно ли, что если все значения дискретной гармонической функции вещественны и неотрицательны, то эта функция постоянна?

Предложенные задачи и теоремы являются дискретными аналогами соответствующих результатов из классической теории потенциала. Цель проекта – продвинуться в построении дискретной теории потенциала на плоскости и в пространстве.

Литература:

1. В.В. Вавилов, А.В. Устинов, Задачи на клетчатой бумаге. – М.: Школа им. А.Н. Колмогорова, 2005.

2. В.В. Вавилов, А.В. Устинов, Многоугольники на решетках. – М.: МЦНМО, 2006.

 

Задача А.Н. Колмогорова о циклах

Научный руководитель:

к.ф.м.н., доцент Вавилов Валерий Васильевич (Школа им. А.Н. Колмогорова)

По любому натуральному числу n можно построить другое натуральное число m по следующему правилу: запишем число n русскими словами и подсчитаем количество затраченных на эту запись букв – это и будет число m. Например, числу n = 1987 (тысяча девятьсот восемьдесят семь) отвечает число m = 30.

Делая такие сопоставления n  m для маленьких n, легко найти те из них, которые «переходят» сами в себя (то есть m=n): это n₁ = 3(три), n₂ = 11(одиннадцать). Однако есть еще тройка замечательных чисел, которые указанным преобразованием переводятся друг в друга по циклу. Это тройка состоит из чисел 4,5 и 6:

4(четыре) - 6(шесть) - 5(пять) - 4(четыре).

А что происходит с другими числами?

Чтобы выяснить это, надо провести многократные итерации указанного преобразования над выбранным числом и выписать получающуюся цепочку чисел. Например,

1987 - 30(тридцать) - 8(восемь) - 6 - 5 - 4 - 6.

Первый же взятый пример привел нас к циклу 6 - 5 - 4 - 6. Конечно, имеется также много чисел, сводящихся и к «неподвижным» точкам n₁ = 3 и n₂ = 11 нашего преобразования. Но все ли числа сводятся в конечном счете к этим неподвижным точкам или к циклу 6 - 5 - 4 - 6?

Полное решение этой задачи состоит в последовательном решении двух более простых задач:

А) Найти все неподвижные точки и циклы указанного преобразования (две неподвижные точки уже найдены).

Б) Доказать, что любое число n с помощью конечного числа итераций сводится к одной неподвижной из неподвижных точек или одному из циклов.

Второе утверждение может показаться сомнительным – тогда попытайтесь опровергнуть его!

Если вы знает какие-нибудь другие языки, порешайте аналогичную задачу и для них. Оказывается, что для любого языка из ныне существующих (даже, быть может, вам неизвестных) можно чисто математическим рассуждениями решить вторую из указанных задач. Заметим, при этом, что все числа, входящие в неподвижные точки и циклы на этих языках не превосходят 100. Почему?

Цель проекта состоит в нахождении оценок на выяснении число шагов (итераций), за которое данное число «превращается» в неподвижную точку или попадает в цикл.

Литература:

1. А.Н. Колмогоров, Математика – наука и профессия. / Сост. Г.А. Гальперин. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 288с. –(Б-чка «Квант». Вып.64).

 

Правильные многоугольники на решетках

Научный руководители:

к.ф.м.н., доцент Вавилов Валерий Васильевич (Школа им. А.Н. Колмогорова, г. Москва)

к.ф.м.н., заведующий отделом теоретической и прикладной математики Хабаровского отделения ИПМ ДВО РАН Устинов Алексей Владимирович

А. Покажите, что ни один правильный многоугольник (за исключением квадрата) нельзя расположить на клетчатой бумаге так, чтобы его вершины находились в узлах клетчатой бумаги.

Б. Покажите, что любой правильный многоугольник можно расположить на клетчатой бумаге так, что его вершины попадут в различные кружки радиусов ɛ с центрами в узлах бумаги (которые нарисованы для каждого узла), 0< ɛ <1/2 .

В. Опишите алгоритм (более быстрый, чем разумный перебор), который позволял бы для данного  > 0 находить правильный треугольник (пятиугольник), с вершинами в -окрестностях точек целочисленной решетки. На рисунках правильный треугольник и правильный пятиугольник находятся внутри жирных контуров.

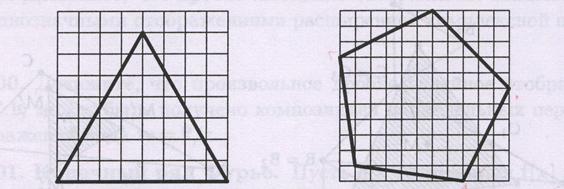
«Почти» правильные многоугольники с вершинами в узлах целочисленной решетки будут обладать различными любопытными свойствами. Например, пятиугольник, изображенный на рисунке, имеет три равные стороны и четыре равных угла.

Цель проекта состоит в описании почти правильных n-угольников, выделив среди них выделить те, которые имеют наименьшие размеры.

Литература

1. Н.Б. Алфутова, А.В. Устинов, Алгебра и теория чисел. Сборник задач. – М.: МЦНМО,2005.

2. В.В. Вавилов, А.В. Устинов, Задачи на клетчатой бумаге. – М.: Школа им. А.Н. Колмогорова, 2005.

3. В.В. Вавилов, А.В. Устинов, Многоугольники на решетках. – М.: МЦНМО, 2006.

 

Геометрия преследования

Научный руководители:

д.ф.м.н, профессор Томский Георгий Васильевич (Франция)

к.ф.м.н, доцент Вавилов Валерий Васильевич (Школа им. А.Н. Колмогорова)

А. В центре поля, имеющего форму квадрата, находится волк, а вершинах квадрата – четыре собаки. Волк может бегать по всему полю, а собаки – только по сторонам квадрата. Известно, что волк задирает собаку, а две собаки задирают волка. Максимальная скорость собаки в 1,5 раза больше максимальной скорости волка. Имеют ли возможность собаки не выпустить волка из квадрата?

Б) На шахматной доске 8 × 8 двое играют в игру «кошки-мышки». У первого одна фишка – мышка, у второго несколько фишек – кошек. Все фишки ходят одинаково: вправо, влево, вверх или вниз на одну клетку. Если мышка оказалась на краю доски, то очередным ходом она спрыгивает с доски. Если кошка и мышка попадают на одну и ту же клетку, то кошка съедает мышку.

Играющие ходят по очереди, причем второй передвигает своим ходом всех своих кошек сразу (разных кошек можно при этом сдвигать в разных направлениях). Начинает мышка. Она старается спрыгнуть с доски, а кошки стараются до этого ее съесть.

1) Пусть кошек всего две. Мышка уже поставлена на какую-то клетку не на краю. Можно ли так поставить кошек на краю доски, чтобы они сумели съесть мышку?

2) Пусть кошек три, но зато мышка имеет лишний ход: в первый раз она делает два хода подряд. Может ли мышка убежать от кошек, каково бы ни было начальное расположение фишек?

Цель проекта состоит в решении этих задач и различных их обобщений (например, изучить возможности «поимки» волка при других соотношениях между скоростями движениями волка и собак в задаче А, куб а не квадрат в той же задаче А и произвольная доска и несколько кошек и мышек в задаче Б).

Литература

1. Г.В. Томский, Элементарная геометрия преследования. – Editiones du JIPTO, France, 2005.

2. Л.А. Петросян, Б.Б. Рихсиев, Преследование на плскости. –М.: Наука, 1991. (Популярные лекции по математике; вып. 61).

 

Целые точки в областях

Научный руководитель:

к.ф.м.н., заведующий отделом теоретической и прикладной математики Хабаровского отделения ИПМ ДВО РАН Устинов Алексей Владимирович

Пусть Ω - плоская область, ограниченная замкнутой несамопересекающейся кривой. Обозначим через S площадь Ω, Р – ее периметр и N – число точек целочисленной решетки Z² (клетчатой бумаги), лежащих внутри Ω. Для любой выпуклой области известно неравенство Ярника

и его уточнение

Следующее утверждение показывает, что требование выпуклости можно отбросить, ослабив формулировку.

Теорема. Справедливо неравенство

Доказательство. Пусть N₁ – число квадратов вида [a,a+1)× [b,b+1) (a,b Z), лежащих внутри Ω, и N₂ – число квадратов, имеющих с Ω хотя бы одну общую точку. Тогда

и, значит,

где М – число квадратов, через которые проходит граница Ω. В каждом из таких квадратов выберем точку A_k (0≤k<M) на границе Ω (нумерация точек – в порядке их следования по границе). Среди любых пяти квадратов, через которые проходит граница Ω, всегда можно выбрать два, замыкания которых не имеют общих точек. Поэтому при любом k длина отрезка границы между точками A_k A_k+1 удовлетворяет неравенству l(A_k, A_k+1) > 1. Отсюда

Значит, М < 4(Р+1) и

Задача для исследования. Выясните, можно ли уточнить константу в доказанной теореме.

Литература:

1. В.В. Вавилов, А.В. Устинов, Задачи на клетчатой бумаге. – М.: Школа им. А.Н. Колмогорова, 2005.

2. В.В. Вавилов, А.В. Устинов, Многоугольники на решетках. – М.: МЦНМО, 2006.

 

Две задачи на метод спуска

Научный руководитель:

к.ф.м.н., заведующий отделом теоретической и прикладной математики Хабаровского отделения ИПМ ДВО РАН Устинов Алексей Владимирович

Задача 1. Найдите все пары натуральных чисел a и b, для каждой из которых

a² + b² + 1 делится на ab.

Решение. Пусть (a,b) – одно из решений и

a² + b² + 1 = nab (n ≥ 1). (1)

Если предположить, что a = b, то сразу получается, что a = b = 1 и n = 3.

Если же a > b, то равенство (1) можно рассматривать как квадратное уравнение относительно а. Поскольку мы знаем, что это уравнение имеет один целый корень а = а₁, то и второй корень этого уравнения

а₂ = (b²+1)/a₁

также будет целым числом. Кроме того, из неравенства а₁ ≥ b + 1 следует, что

а₂ = (b²+1)/a₁<=b<a₁

Таким образом, из одного решения (а₁,b) мы можем перейти к другому (а₂, b) с меньшей суммой. Этот процесс может закончиться только тогда, когда a = b. Поэтому n = 3 и мы имеем дело с уравнением

a² + b² + 1 = 3ab.

Спуск (a, b) → (b, nb –a) = (b, 3b-a) обязательно приводит к паре (1,1), поэтому все решения могут быть получены из пары (a,b) = (1,1) с помощью рекуррентных соотношений

b_k+1 = a_k ,

a_k+1 = 3b_k – a_k.

Следовательно, мы имеем дело с последовательностью

(1,1), (2,1), (5,2), (13,5), (34,13), … , (F_2k-1, F_2k+1),... ,

где F_k - числа Фибоначчи, определяемые начальными условиями F₀=1, F₁=1 и рекуррентным соотношением F_k+2=F_k+1+F_k

Задача 2. (IMO, 1986.6) Для некоторых целых неотрицательных a и b число m=(a²+b²)/(ab+1)

оказалось целым. Докажите, что m – полный квадрат.

Решение. Будем считать, что a ≥ b ≥ 0.

Если b = 0, то m = a² и утверждение задачи очевидно.

Если же b > 0, то перейдем к квадратному уравнению относительно а: a²+b²=m(ab+1)

Один из его корней (а = а₁) – целое число. По теореме Виета второй корень a₂=mb-a₁=(b²-m)/a₁<a₁

также будет целым числом. Кроме того, m=(a²+b²)/(ab+1)>(a-1)/b

и значит, m>=a/b=a₁/b и a₂=mb-a₁>=0

Таким образом, по паре (а₁, b) построена пара решений (а₂, b) с наименьшей суммой. Следовательно, в конце концов мы дойдем до пары, в которой одна из переменных равна нулю.

Задачи для исследования.

Задача 3. Изучите множества пар натуральных чисел (a,b) , для которых

a² + b² + m делится на ab,

где m = ± 1, ± 2, ... – некоторое целое число.

Задача 4. Пусть a,b – натуральные и для данного числа n ≥ 2 оказалось, что m=(a²+b²)/(ab+n) - целое число. Что можно сказать о числе m?

Проекция ломаной

Научный руководитель:

к.ф.м.н., доцент Шарыгин Георгий Игоревич (Школа им. А.Н. Колмогорова)

Единичный куб разбит на n маленьких кубиков. Рассмотрим ломаную,

а) ребра которой совпадают с ребрами кубиков;

б) вершины которой совпадают с вершинами маленьких кубиков, а звенья ломаной могут быть диагоналями кубиков, или их граней;

в) вершины которой совпадают с вершинами маленьких кубиков, а о звеньях ничего неизвестно вообще.

Рассмотрим её проекции на три координатные плоскости. Получаются 3 набора
отрезков на плоскости.

Когда ломаная восстанавливается по этим наборам? Когда такое восстановление единственное? Для каких наборов рисунков такое восстановление существует?

Наконец, можно попытаться ответить на тот же самый вопрос, когда вместо ломаной мы рассматриваем произвольный граф вписанный в куб.

Описанные многоугольники

Научный руководитель:

к.ф.м.н., доцент Шарыгин Георгий Игоревич (Школа им. А.Н. Колмогорова)

Известно, что в 4-угольник можно вписать окружность тогда и только тогда, когда

суммы его противоположных сторон равны между собой. Но это не единственное
условие, эквивалентное существованию вписанной окружности. Например, можно
продлить его противоположные стороны до пересечения и рассмотреть суммы длин
получающихся отрезков. С другой стороны, для 6-, 8- и т. д. (четно-)угольников, условие на сумму сторон (сумма длин четных сторон равна сумме длин нечетных сторон) является, очевидно, необходимым, но не достаточным условием описанности.

Задача состоит в отыскании достаточного условия существования вписанной в такой многоугольник окружности.

Гипотеза состоит в том, что для этого надо к условию типа суммы сторон добавить
какое-то условие о сумме длин продолжений. Отдельный вопрос – существование
окружности, вписанной в нечетноугольники, например, в 5-угольник.

Литература

1. Г.С.М. Коксетер, С.Л. Грейтцер, Новые встречи с геометрией, - М.: Наука, 1978.

2. И. Ф. Шарыгин, Задачи по планиметрии. –М.: Наука,

3. Д.О. Шклярский, Н.Н. Ченцов, И.М. Яглом, Избранные задачи и теоремы элементарной математики. – М.: Наука, 1977.

Контактное число треугольника (тетраэдра)

Научный руководитель:

к.ф.м.н., доцент Шарыгин Георгий Игоревич (Школа им. А.Н. Колмогорова)

Напомним, что контактным числом (выпуклой) фигуры называется максимальное
число непересекающихся равных ей фигур, которые можно к ней «прислонить»,
т.е. разместить на плоскости (или в пространстве) так, чтобы они касались
данной фигуры. Известно, что контактное число круга равно 6 (очевидный факт),
а контактное число шара равно 12 (теорема о 13 шарах).

Требуется оценить контактное число простейшего многоугольника-треугольника.

Представляется очевидным, что оно должно зависеть от отношения его наибольшей и наименьшей сторон. От каких еще параметров оно зависит?

Можно ли написать какую-нибудь функцию от этих параметров, которая оценивала
бы контактное число фигуры сверху или снизу?

Еще более интересным представляется аналогичный вопрос, когда треугольник заменен на тетраэдр (или даже более общие многоугольники или многогранники).

Литература

1. Д.О. Шклярский, Н.Н. Ченцов, И.М. Яглом, Геометрические оценки и задачи из комбинаторной геометрии. – М.: Наука, 1974.

2. Б. А. Кордемский, Н.В. Руслаев, Удивительный квадрат. – М.-Л.: Гостехиздат, 1952.

Проблема Лебега для четырехугольника

Научный руководитель:

к.ф.м.н., доцент Шарыгин Георгий Игоревич (Школа им. А.Н. Колмогорова)

Знаменитая проблема Лебега об отыскании наименьшей (выпуклой) покрышки для
(выпуклой) фигуры фиксированного диаметра стоит уже более ста лет. С другой
стороны, в 1980-х годах был получен ответ на упрощенный вариант этой задачи:
найти наименьшую выпуклую покрышку для любого треугольника, чей диаметр не
превосходит 1. Ответ оказался достаточно неожиданным: площадь такой покрышки (она оказалась треугольной), например, равна ½cos10(град). Еще удивительнее, что результат можно еще улучшить, если рассматривать невыпуклые фигуры!

Предлагается попытаться сделать следующий шаг в направлении общей проблемы Лебега:

Найти наименьшую (выпуклую) покрышку 4-угольников. Для начала стоит рассмотреть лишь ограниченный класс многоугольников, например, параллелограммы, трапеции или дельтоиды (многоугольники с перпендикулярными диагоналями).

Литература

1. Д.О. Шклярский, Н.Н. Ченцов, И.М. Яглом, Геометрические оценки и задачи из комбинаторной геометрии. – М.: Наука, 1974.