LXX Московская Математическая олимпиада

Подведены итоги LXX Московской математической олимпиады.

Поздравляем школьников СУНЦ МГУ, успешно выступивших на олимпиаде:

Условия задач олимпиады

10 класс

1. На сторонах единичного квадрата отметили точки K, L, M и N так, что прямая KM параллельна двум сторонам квадрата, а прямая LN — двум другим сторонам квадрата. Отрезок KL отсекает от квадрата треугольник периметра 1. Треугольник какой площади отсекает от квадрата отрезок MN?

2. Можно ли покрасить 15 отрезков, изображенных на рисунке, в 3 цвета так, чтобы никакие 2 отрезка одного цвета не имели общего конца?

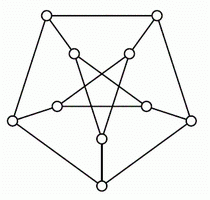3. Существуют ли такие натуральные числа x и y, что x²+x+1 является натуральной степенью y, а y²+y+1 — натуральной степенью x?

4. Капитан Врунгель в своей каюте раскладывает пасьянс. Перетасованная колода из 52 карт разложена по кругу, одно место свободно. Матрос Фукс, не отходя от штурвала и не зная начальной раскладки, называет карту. Если эта карта лежит рядом со свободным местом, Врунгель передвигает ее на это место, не сообщая Фуксу. Иначе ничего не происходит. Потом Фукс называет еще одну карту, Врунгель совершает аналогичное действие, и так сколько угодно раз, пока Фукс не скажет «хватит». Фукс выиграет, если скажет «хватит» в тот момент, когда каждая карта окажется не на том месте, на котором была вначале. Может ли Фукс выиграть наверняка?

5. Треугольник ABC вписан в окружность с центром в O. X — произвольная точка внутри треугольника ABC, такая, что ∠XAB=∠XBC=φ, а P — такая точка, что PX⊥ OX, ∠XOP=φ, причем углы ∠XOP и ∠XAB одинаково ориентированы. Доказать, что все такие точки P лежат на одной прямой.

6. С ненулевым числом разрешается проделывать следующие операции:

Верно ли, что из каждого ненулевого рационального числа можно получить каждое рациональное число с помощью конечного числа таких операций?

1. Круглая мишень разбита на 20 секторов, которые нумеруются по кругу в каком-либо порядке числами 1, 2,…, 20. Если секторы занумерованы, например (как при игре в дартс), в следующем порядке 1, 20, 5, 12, 9, 14, 11, 8, 16, 7, 19, 3, 17, 2, 15, 10, 6, 13, 4, 18, то наименьшая из разностей между номерами соседних (по кругу) секторов равна 12–9=3 (из большего числа вычитается меньшее). Может ли указанная величина при нумерации в другом порядке быть больше 3? Каково наибольшее возможное значение этой величины?

2. Значение a подобрано так, что число корней первого из уравнений

3. Каким может быть произведение нескольких различных простых чисел, если оно кратно каждому из них, уменьшенному на 1? Найдите все возможные значения этого произведения.

Примечание. В распечатанных для участников олимпиады вариантах эта задача была сформулирована чуть иначе.

3. Каким может быть произведение N нескольких различных простых чисел, если оно кратно каждому из них, уменьшенному на 1? Найдите все возможные значения N.

Возникающая неточность понимания была специально откомментирована во всех аудиториях.

4. Точка O лежит в основании A₁A₂…A_n пирамиды SA₁A₂… A_n, причем SA₁=SA₂=…=SA_n и ∠SA₁O=∠SA₂O=…=∠SA_nO. При каком наименьшем значении n отсюда следует, что SO — высота пирамиды?

5. Квадрат состоит из n x n клеток: две противоположные угловые клетки — черные, а остальные — белые. Какое наименьшее количество белых клеток достаточно перекрасить в черный цвет, чтобы после этого с помощью преобразований, состоящих в перекрашивании всех клеток какого-либо столбца или какой-либо строки в противоположный цвет, можно было сделать черными все клетки этого квадрата?

6. Точки A', B' и C' — середины сторон BC, CA и AB треугольника ABC соответственно, а BH — его высота. Докажите, что если описанные около треугольников AHC' и CHA' окружности проходят через точку M, отличную от H, то ∠ABM=∠CBB'.

7. Миша мысленно расположил внутри данного круга единичного радиуса выпуклый многоугольник, содержащий центр круга, а Коля пытается угадать его периметр. За один шаг Коля указывает Мише какую-либо прямую и узнает от него, пересекает ли она многоугольник. Имеет ли Коля возможность наверняка угадать периметр многоугольника:

а) через 3 шага с точностью до 0,3;
б) через 2007 шагов с точностью до 0,003?

На отбор в команду г. Москвы на заключительном этапе Всероссийской олимпиады школьников по математике приглашены:

10 класс: Каниськин Сергей, Кисловская Анна, Шапичев Алексей;

11 класс: Погудин Глеб, Тихонов Юлий, Андреев Александр.

Подробную информацию о Московской математической олимпиаде можно найти на сайте http://olympiads.mccme.ru/mmo/.