Главная » Новости » Соревнования » Московская математическая регата 10-х классов
Московская математическая регата 10-х классов
7 марта 2009 года состоялась Московская математическая регата 10 классов. В регате приняли участие около 60 команд сильнейших школ Москвы, а также команды г. Кострома, г. Переславль Залесский Ярославской области, г. Долгопрудный Московской области, г. Селятино Московской области, г. Королев Московкой области.
Официальная страница РЕГАТ: http://olympiads.mccme.ru/regata/.
В регате приняли участие 3 команды СУНЦ МГУ:
- "СУНЦ А" (состав: Латыпов Родион (10Б), Лесота Олег (10Б), Постолит Егор (10Б), Рябченко Константин (10Б))
- "СУНЦ Б" (состав: Ивлев Федор (10Б), Горбань Степан (10Б), Беляков Сергей (10Б), Голова Анна (10Б))
- "СУНЦ В" (состав: Андреев Роман (10В), Косолапов Кирилл (10В), Кондратьев Михаил (10В), Макаров Александр (10Б))
Команда "СУНЦ Б" заняла 1 абсолютное место (диплом I степени), команда "СУНЦ В" разделила с командрой школы "ИНТЕЛЛЕКТУАЛ" 4-5 место (диплом II степени), команда "СУНЦ А" заняла 13 место (дплом III степни).
|
Команда |
I тур |
II тур |
III тур |
IV тур |
V тур |
Сумма |
Диплом | ||||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|||
|
СУНЦ Б |
2 |
6 |
6 |
2 |
7 |
0 |
8 |
8 |
8 |
9 |
9 |
1 |
7 |
7 |
6 |
86 |
I |
|
5 7 |
6 |
0 |
6 |
7 |
7 |
0 |
8 |
8 |
0 |
5 |
9 |
9 |
7 |
7 |
5 |
84 |
I |
|
1 5 1 4 А |
6 |
6 |
6 |
7 |
7 |
7 |
0 |
8 |
7 |
9 |
9 |
0 |
0 |
0 |
6 |
78 |
II |
|
Интеллектуал Б |
6 |
0 |
6 |
7 |
7 |
1 |
8 |
8 |
0 |
8 |
9 |
1 |
0 |
7 |
7 |
75 |
II |
|
СУНЦ В |
6 |
0 |
6 |
7 |
7 |
7 |
8 |
8 |
0 |
5 |
9 |
0 |
0 |
5 |
7 |
75 |
II |
|
2 А |
6 |
6 |
6 |
7 |
7 |
7 |
8 |
8 |
0 |
0 |
0 |
1 |
4 |
0 |
7 |
67 |
III |
|
2 Е |
6 |
3 |
6 |
7 |
7 |
0 |
8 |
0 |
0 |
7 |
9 |
0 |
0 |
7 |
7 |
67 |
III |
|
Кострома А |
6 |
6 |
6 |
7 |
0 |
6 |
2 |
8 |
8 |
9 |
0 |
1 |
0 |
0 |
7 |
66 |
III |
|
5Б Долгопрудный |
0 |
0 |
6 |
7 |
7 |
1 |
0 |
8 |
0 |
0 |
9 |
9 |
0 |
7 |
7 |
61 |
III |
|
2 Б |
6 |
6 |
6 |
7 |
3 |
0 |
0 |
8 |
8 |
0 |
0 |
0 |
0 |
7 |
7 |
58 |
III |
|
2 Г |
6 |
0 |
6 |
7 |
7 |
1 |
-1 |
0 |
8 |
7 |
9 |
0 |
0 |
0 |
7 |
57 |
III |
|
2 1 8 |
3 |
6 |
7 |
6 |
0 |
8 |
8 |
0 |
0 |
9 |
0 |
0 |
0 |
7 |
54 |
III | |
|
СУНЦ А |
6 |
6 |
5 |
5 |
2 |
8 |
8 |
3 |
0 |
1 |
0 |
0 |
7 |
51 |
III | ||
|
2 Д |
6 |
0 |
6 |
7 |
1 |
0 |
0 |
8 |
7 |
0 |
0 |
9 |
0 |
0 |
2 |
46 |
ПП |
|
2 В |
6 |
4 |
6 |
7 |
0 |
0 |
4 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
42 |
ПП |
|
1 5 5 4 |
6 |
3 |
6 |
0 |
0 |
0 |
2 |
1 |
4 |
0 |
9 |
0 |
0 |
7 |
3 |
41 |
ПП |
|
1 5 1 4 Б |
6 |
0 |
6 |
2 |
2 |
1 |
0 |
8 |
8 |
0 |
0 |
0 |
0 |
7 |
40 |
ПП | |
|
5 4 А |
4 |
0 |
6 |
2 |
0 |
3 |
8 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
38 |
|
|
3 1 5 Б |
6 |
0 |
6 |
7 |
0 |
0 |
0 |
3 |
0 |
9 |
0 |
7 |
0 |
38 |
|||
|
1 5 4 3 Г |
6 |
0 |
6 |
2 |
7 |
0 |
0 |
8 |
0 |
8 |
0 |
0 |
0 |
0 |
1 |
38 |
|
|
Интеллектуал А |
6 |
0 |
6 |
2 |
7 |
0 |
1 |
8 |
1 |
4 |
0 |
1 |
0 |
0 |
1 |
37 |
|
|
1 7 9 А |
6 |
3 |
6 |
0 |
0 |
0 |
4 |
0 |
8 |
0 |
0 |
1 |
7 |
0 |
0 |
35 |
|
|
1 5 4 3 В |
2 |
4 |
6 |
7 |
1 |
0 |
0 |
3 |
8 |
0 |
0 |
1 |
0 |
0 |
1 |
33 |
|
|
Переславль |
2 |
0 |
6 |
2 |
3 |
0 |
2 |
0 |
8 |
0 |
9 |
1 |
0 |
0 |
0 |
33 |
|
|
1 5 6 7 |
2 |
3 |
6 |
7 |
7 |
1 |
0 |
0 |
4 |
0 |
0 |
1 |
0 |
0 |
1 |
32 |
|
|
1 5 4 3 Б |
2 |
0 |
6 |
7 |
7 |
0 |
0 |
8 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
31 |
|
|
1 7 9 Б |
6 |
3 |
6 |
2 |
2 |
0 |
0 |
8 |
0 |
3 |
0 |
0 |
0 |
0 |
0 |
30 |
|
|
5А Долгопрудный |
2 |
0 |
6 |
2 |
1 |
7 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
7 |
26 |
|
|
5 4 В |
2 |
6 |
0 |
7 |
0 |
0 |
0 |
0 |
3 |
0 |
1 |
0 |
0 |
7 |
26 |
||
|
6 5 4 |
6 |
3 |
6 |
0 |
2 |
7 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
26 |
|
|
1 5 4 3 А |
2 |
4 |
6 |
0 |
7 |
0 |
0 |
0 |
0 |
3 |
0 |
1 |
0 |
0 |
1 |
24 |
|
|
2 0 0 7 Ж |
0 |
0 |
6 |
2 |
7 |
0 |
0 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
24 |
||
|
2 0 0 7 В |
6 |
0 |
6 |
2 |
2 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
0 |
0 |
3 |
23 |
|
|
1 1 8 9 А |
1 |
7 |
0 |
2 |
0 |
0 |
3 |
0 |
0 |
7 |
0 |
1 |
21 |
||||
|
2 0 0 7 А |
6 |
0 |
0 |
3 |
1 |
0 |
8 |
0 |
3 |
0 |
0 |
0 |
0 |
0 |
21 |
||
|
2 0 0 7 Б |
6 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
1 |
0 |
0 |
0 |
21 |
|
|
5В Долгопрудный |
2 |
0 |
6 |
2 |
2 |
0 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
21 |
|
|
1 5 3 7 Б |
6 |
0 |
6 |
7 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
20 |
|
|
1 5 5 7 А |
2 |
6 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
0 |
19 |
||
|
2_1237 |
0 |
3 |
6 |
0 |
4 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
2 |
17 |
|
|
1 5 1 1 А |
2 |
2 |
6 |
2 |
2 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
17 |
|
|
2 0 0 7 Г |
2 |
0 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
17 |
|
|
2 0 0 7 Д |
6 |
0 |
0 |
7 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
15 |
|
|
Селятино |
6 |
0 |
6 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
14 |
|
|
1 5 1 1 Б |
0 |
4 |
6 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
13 |
|
|
1 7 9 В |
1 |
0 |
6 |
2 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
12 |
|
|
1 5 3 7 А |
2 |
0 |
0 |
2 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
11 |
|
|
7 Б |
0 |
0 |
6 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
10 |
|
|
1 1 8 9 Б |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
8 |
||||
|
3 1 5 А |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
7 |
|
|
7 А |
0 |
0 |
2 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
|
|
1 5 1 1 В |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
0 |
0 |
0 |
5 |
|
|
1 5 6 4 А |
2 |
0 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
|
|
Королев |
0 |
0 |
1 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
|
1 3 0 2 |
2 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
|||
|
1 5 6 4 Б |
0 |
0 |
2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
|
|
2 0 0 7 Е |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
||
|
1918 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Первый тур (10 минут; каждая задача — 6 баллов).
1.1. Найдите значение выражения ![]() , если x2 + y2 = 6xy и x ¹ y.
, если x2 + y2 = 6xy и x ¹ y.
Второй тур (15 минут; каждая задача — 7 баллов).
2.1. Решите систему уравнений: 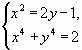 .
.
2.2. Найдите наибольший периметр параллелограмма, диагонали которого 6 см и 8 см.
Третий тур (20 минут; каждая задача — 8 баллов).
Четвертый тур (25 минут; каждая задача — 9 баллов).
4.1. Пусть an – целое число, ближайшее к ![]() . Найдите все такие натуральные n, что
. Найдите все такие натуральные n, что ![]() .
.
Пятый тур (15 минут; каждая задача — 7 баллов).
5.3. Найдите все целые решения уравнения k(k + 1) = n3.