Главная » Новости » Соревнования » Московская математическая регата 11-х классов
Московская математическая регата 11-х классов
06.12.2008, 6 декабря 2008 года состоялась Московская математическая регата 11 классов. В регате приняли участие около 50 команд сильнейших школ Москвы, а также команды г. Переславль Залесский Ярославской области, г. Троицк Московской области, г. Королев Московской области.
Официальная страница РЕГАТ: http://olympiads.mccme.ru/regata/.
В регате приняли участие 5 команд СУНЦ МГУ, составленные из школьников 10 и 11 классов:
По дороге на регату мы попали в "пробку" и пропустили целиком 1 тур и значительную часть второго тура (спасибо организаторам, нас пустили в середине вторго тура). Такая фора соперникам не помешала команде "СУНЦ А" одержать победу, но, к сожалению, преодолеть гроссмейстерский рубеж в 100 очков опять не получилось (в 2008 году та же команда заняла 1 место в регате 10-х классов, не добрав до сотни 4 баллов).
- "СУНЦ А" (состав: Радонец Алексей (11Б), Немиро Владислав (11Б), Ярославцев Иван (11Б), Тренин Кирилл (11Б)) - АБСОЛЮТНЫЙ победитель регаты
- "СУНЦ Б" (3 мето, диплом II степени), "СУНЦ В" , "СУНЦ Г" (6 место, диплом III степени), "СУНЦ Д"
|
Команда |
I тур |
II тур |
III тур |
IV тур |
V тур |
Сумма |
Диплом | ||||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|||
|
СУНЦ А |
7 |
7 |
7 |
8 |
8 |
6 |
9 |
9 |
9 |
7 |
7 |
7 |
91 |
I | |||
|
1 5 4 3 А |
6 |
6 |
6 |
7 |
7 |
7 |
8 |
7 |
0 |
0 |
0 |
9 |
0 |
7 |
7 |
77 |
II |
|
СУНЦ Б |
7 |
7 |
7 |
8 |
8 |
0 |
9 |
0 |
9 |
7 |
7 |
7 |
76 |
II | |||
|
Переславль |
6 |
6 |
6 |
7 |
7 |
7 |
8 |
0 |
8 |
0 |
0 |
3 |
7 |
0 |
7 |
72 |
II |
|
2 0 0 7 А |
6 |
6 |
6 |
7 |
7 |
7 |
0 |
0 |
0 |
5 |
9 |
0 |
0 |
7 |
7 |
67 |
III |
|
СУНЦ Г |
7 |
4 |
7 |
8 |
8 |
8 |
0 |
0 |
9 |
0 |
7 |
7 |
65 |
III | |||
|
1 9 2 |
6 |
6 |
6 |
7 |
7 |
0 |
4 |
0 |
3 |
0 |
0 |
4 |
7 |
7 |
7 |
64 |
III |
|
Квантик А |
6 |
6 |
6 |
0 |
7 |
7 |
8 |
0 |
7 |
0 |
0 |
3 |
0 |
7 |
7 |
64 |
III |
|
2 Г |
6 |
6 |
1 |
7 |
7 |
7 |
8 |
0 |
0 |
0 |
0 |
3 |
0 |
7 |
7 |
59 |
ПП |
|
1 7 9 В |
6 |
6 |
2 |
7 |
7 |
0 |
8 |
0 |
0 |
0 |
0 |
9 |
0 |
7 |
7 |
59 |
ПП |
|
1 1 8 9 Б |
6 |
6 |
6 |
7 |
7 |
0 |
8 |
0 |
0 |
0 |
0 |
3 |
0 |
7 |
7 |
57 |
ПП |
|
2 0 0 7 Д |
6 |
6 |
6 |
7 |
7 |
7 |
0 |
0 |
0 |
0 |
0 |
2 |
7 |
7 |
0 |
55 |
ПП |
|
2 0 0 7 Г |
6 |
0 |
6 |
7 |
1 |
7 |
8 |
0 |
0 |
0 |
0 |
3 |
0 |
7 |
7 |
52 |
ПП |
|
1 7 9 Г |
5 |
5 |
6 |
7 |
5 |
7 |
-1 |
0 |
0 |
1 |
0 |
3 |
0 |
6 |
7 |
51 |
ПП |
|
3 1 5 Б |
5 |
6 |
0 |
0 |
7 |
7 |
8 |
0 |
0 |
0 |
0 |
3 |
0 |
7 |
7 |
50 |
ПП |
|
5 7_1 7 9 |
6 |
6 |
0 |
7 |
7 |
7 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
48 |
ПП |
|
3 1 5 А |
6 |
6 |
0 |
7 |
6 |
0 |
0 |
0 |
6 |
0 |
3 |
7 |
7 |
0 |
48 |
ПП | |
|
1 1 8 9 В |
6 |
6 |
6 |
7 |
7 |
0 |
8 |
1 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
48 |
ПП |
|
1 1 8 9 А |
6 |
6 |
0 |
7 |
7 |
0 |
8 |
0 |
0 |
4 |
0 |
1 |
0 |
7 |
0 |
46 |
ПП |
|
1 5 4 3 Б |
6 |
6 |
6 |
7 |
6 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
46 |
ПП |
|
2 Б |
6 |
6 |
0 |
7 |
7 |
6 |
0 |
0 |
6 |
0 |
0 |
0 |
0 |
7 |
0 |
45 |
ПП |
|
СУНЦ Д |
7 |
7 |
0 |
8 |
0 |
8 |
0 |
0 |
0 |
7 |
0 |
7 |
44 |
ПП | |||
|
9 1 А |
6 |
6 |
6 |
7 |
7 |
2 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
7 |
43 |
|
|
1 5 1 1 |
6 |
0 |
6 |
7 |
7 |
7 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
7 |
43 |
|
|
Интеграция |
6 |
0 |
0 |
7 |
7 |
7 |
1 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
7 |
38 |
|
|
5 4 В |
6 |
0 |
0 |
7 |
7 |
0 |
8 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
7 |
36 |
|
|
1 4 3 4 А |
0 |
7 |
7 |
0 |
8 |
0 |
0 |
0 |
0 |
7 |
0 |
7 |
36 |
||||
|
2 0 0 7 Б |
6 |
0 |
6 |
7 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
33 |
|
|
Троицк |
6 |
6 |
2 |
7 |
7 |
0 |
1 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
31 |
|
|
1 1 8 9 Д |
7 |
0 |
7 |
8 |
0 |
0 |
0 |
2 |
0 |
0 |
7 |
31 |
|||||
|
СУНЦ В |
0 |
7 |
7 |
8 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
7 |
30 |
||||
|
7 Б |
0 |
6 |
0 |
7 |
6 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
28 |
|
|
1 5 8 0 |
6 |
6 |
3 |
0 |
7 |
0 |
1 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
26 |
|
|
5 4 А |
5 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
25 |
|
|
2 0 0 7 В |
6 |
6 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
3 |
7 |
23 |
||
|
9 7 8 |
5 |
6 |
0 |
0 |
7 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
19 |
|
|
1 1 8 9 Г |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
7 |
0 |
7 |
18 |
|
|
Квантик Б |
0 |
0 |
6 |
0 |
1 |
7 |
1 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
17 |
|
|
Королев |
6 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
10 |
|
|
2 0 0 7 Е |
1 |
0 |
1 |
7 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
10 |
|
|
7 А |
1 |
6 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
|
|
1 5 6 4 А |
0 |
0 |
1 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
|
|
1 7 1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
||
|
1 5 6 4 Б |
0 |
0 |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Условия задач
Первый тур (10 минут; каждая задача — 6 баллов).
1.1. Пусть 0 < x < 
и 0 < y < . Докажите, что xcosx + ycosy <= ycosx + xcosy.
, 
, 
составили тетраэдр. Какое наибольшее количество граней может оказаться прямоугольными треугольниками?Второй тур (15 минут; каждая задача — 7 баллов).
2.1. Существует ли многочлен Р(x) ненулевой степени с целыми коэффициентами такой, что 
= 2008?
Третий тур (20 минут; каждая задача — 8 баллов).
3.2. Внутри квадрата АВСD выбрана точка K такая, что угол KBC равен углу KDB = a. Найдите угол KAD.
Четвертый тур (25 минут; каждая задача — 9 баллов).
4.1. При каких b найдутся такие a, что система уравнений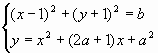 
имеет хотя бы одно решение?
, если известно, что угол AID – прямой. Пятый тур (15 минут; каждая задача — 7 баллов).
5.1. Имеет ли уравнение 
= 
целые корни?